¶ Mathématiques : Généralités sur les fonctions - Exercices
Niveau : 2nde Bac Pro
¶ 1. Comprendre ce qu’est une fonction
On considère la fonction définie par :
- Calculer , et .
- Donner un nombre tel que .
¶ 2. Représentation par tableau de valeurs
On considère la fonction définie par :
- Complèter le tableau de valeurs ci-dessous :
| -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|
- Représenter la fonction sur Geogebra.
- Observer la courbe : est-elle croissante, décroissante ? Expliquer.
¶ 3. Lecture graphique d’une fonction
On donne ci-dessous la représentation d’une fonction .

- Donner l’image de .
- Donner l’image de .
- Donner un antécédent du nombre .
¶ 4. Identifier les variations d’une fonction
On considère la fonction définie par :
- Calculer , et .
- Tracer la droite représentative de la fonction sur Geogebra.
- La fonction est-elle croissante ou décroissante ? Justifier.
¶ 5. Étude des variations à partir d’un graphique
On te donne la représentation graphique de la fonction suivante :
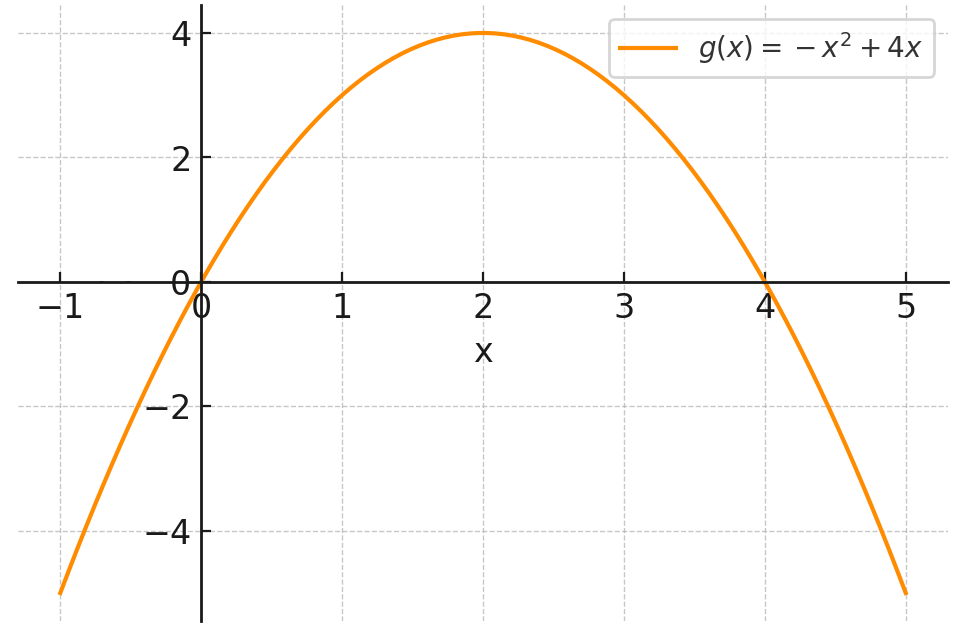
- Sur quel intervalle est-elle croissante ?
- Sur quel intervalle est-elle décroissante ?
- Indiquer les coordonnées du maximum de la fonction.
- Donner les coordonnées d’un minimum, s’il existe.
¶ 6. Exercice de synthèse
On considère la fonction définie sur l'intervale par :
- Calculer , , , et .
- Créer le tableau de valeurs.
- Tracer la courbe représentative sur Geograbra.
- Créer le tableau de variation de cette fonction.
¶ 7. Lecture et interprétation d’une courbe
On donne la courbe représentative d’une fonction .
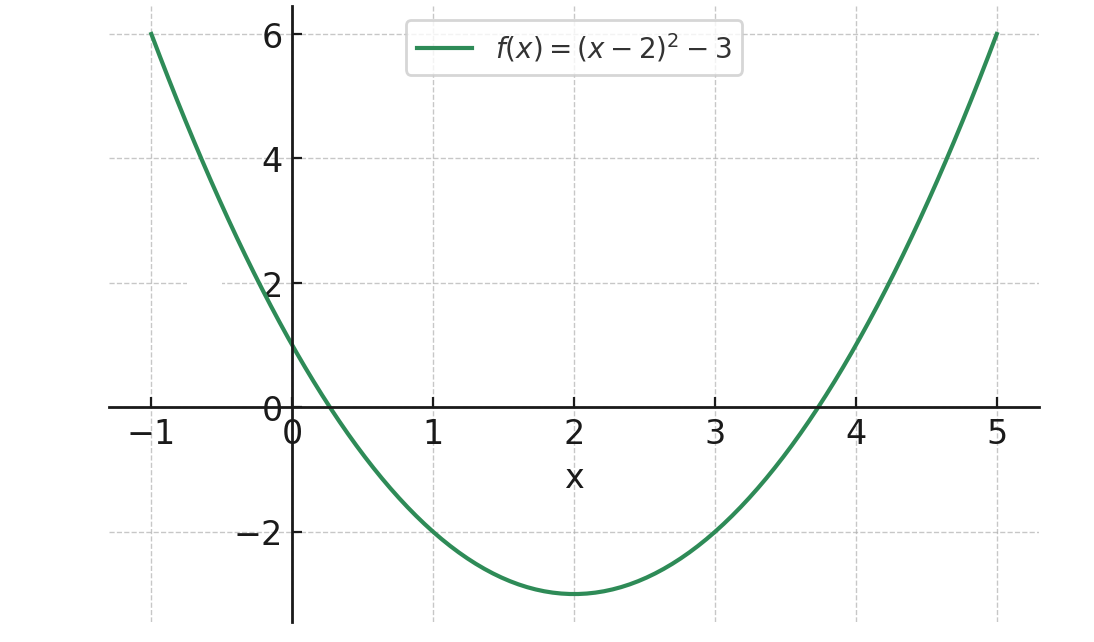
- Indiquer l’image de , et .
- Pour quelle(s) valeur(s) de a-t-on ?
- Créer le tableau de variation de la fonction .
¶ 8. Fonctions et situations concrètes
Une fonction donne le coût total (en euros) d’une activité en fonction du nombre d’élèves inscrits.
Elle est définie par :
- Calculer , et .
- Expliquer ce que représente le nombre dans la situation.
- Représenter graphiquement la fonction sur Geogebra pour entre 0 et 20.
- La fonction est-elle croissante ou décroissante ?
¶ 9. Étude d’une fonction quadratique
On considère la fonction définie par :
- Calculer , , , , , et .
- Tracer la courbe représentative de .
- Indiquer les intervalles de croissance et de décroissance.
- Donner les coordonnées du minimum.
¶ 10. Exercices de réinvestissement
On donne les trois fonctions suivantes :
- Tracer sur Geogebra les trois fonctions.
- Comparer les trois fonctions :
- Quelle est la plus grande pour ?
- Quelle est la plus petite pour ?
Contenu généré avec l’aide de ChatGPT, révisé et adapté par Thibaut Meunier.
Licence : CC BY-SA 4.0