¶ Mathématiques : Fonctions affines et systèmes - Exercices (2ème série)
Niveau : 2nde Bac Pro
¶ Exercice 1 – Refroidissement d’un biberon
Un biberon sort du chauffe-biberon à 70°C.
Il refroidit régulièrement de 2°C par minute.
On note la température (en °C) en fonction du temps (en minutes).
-
Déterminer la température du biberon au bout de : 1 minute, 2 minutes
-
L'ordonné à l'origine de la fonction correspondant à la température du biberon sortant du four. Déterminer
-
Le coefficient directeur de la fonction correspond à la chute de température chaque minute. Déterminer .
-
Déterminer l’expression de .
-
Calculer : et .
-
Tracer sur Geogebra la fonction .
-
Déterminer graphiquement le temps au bout duquel la température 40°C ?
¶ Exercice 2 – Consommation de solution hydroalcoolique
Un distributeur contient au départ 5000 mL.
Chaque soignant utilise 20 mL par entrée.
La quantité restante est modélisée par la fonction :
représente le nombre de personne qui entre dans la pièce
-
Calculer la quantité restante après : 50 utilisations, 150 utilisations
-
Placer les deux points correspondants sur le graphique et tracer la droite représentative de la fonction.
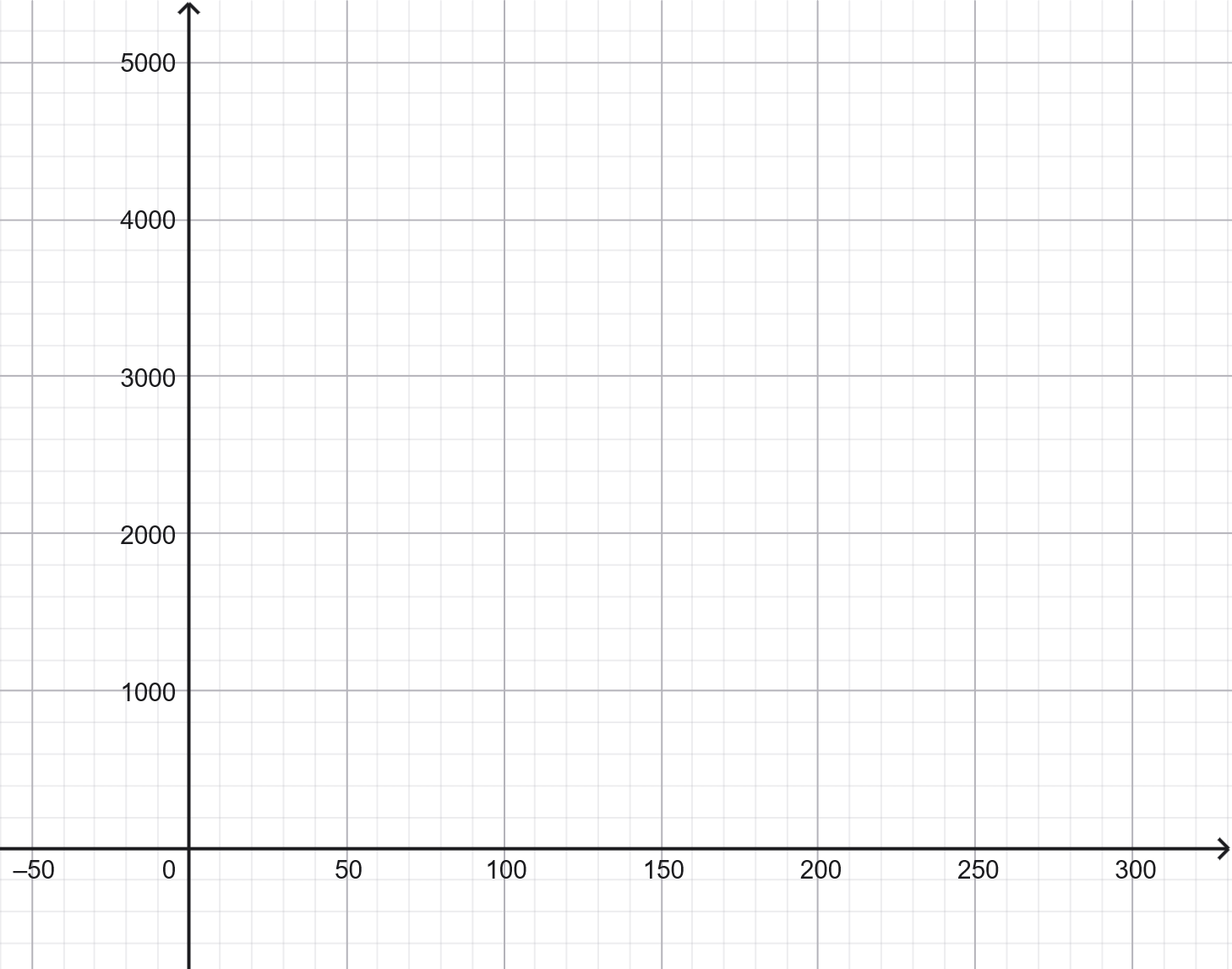
- A l'aide de votre graphique, déterminer à partir de combien d’utilisations le distributeur sera-t-il vide ?
¶ Exercice 3 – Coût des déplacements d’une aide à domicile
Une aide à domicile utilise sa voiture pour se rendre chez les personnes.
Le coût du trajet est modélisé par :
représente la distance en kilomètre
- Compléter le tableau :
| Distance (km) | 0 | 4 | 10 | 20 |
|---|---|---|---|---|
| Coût (€) |
- Tracer la droite correspondant à cette fonction.
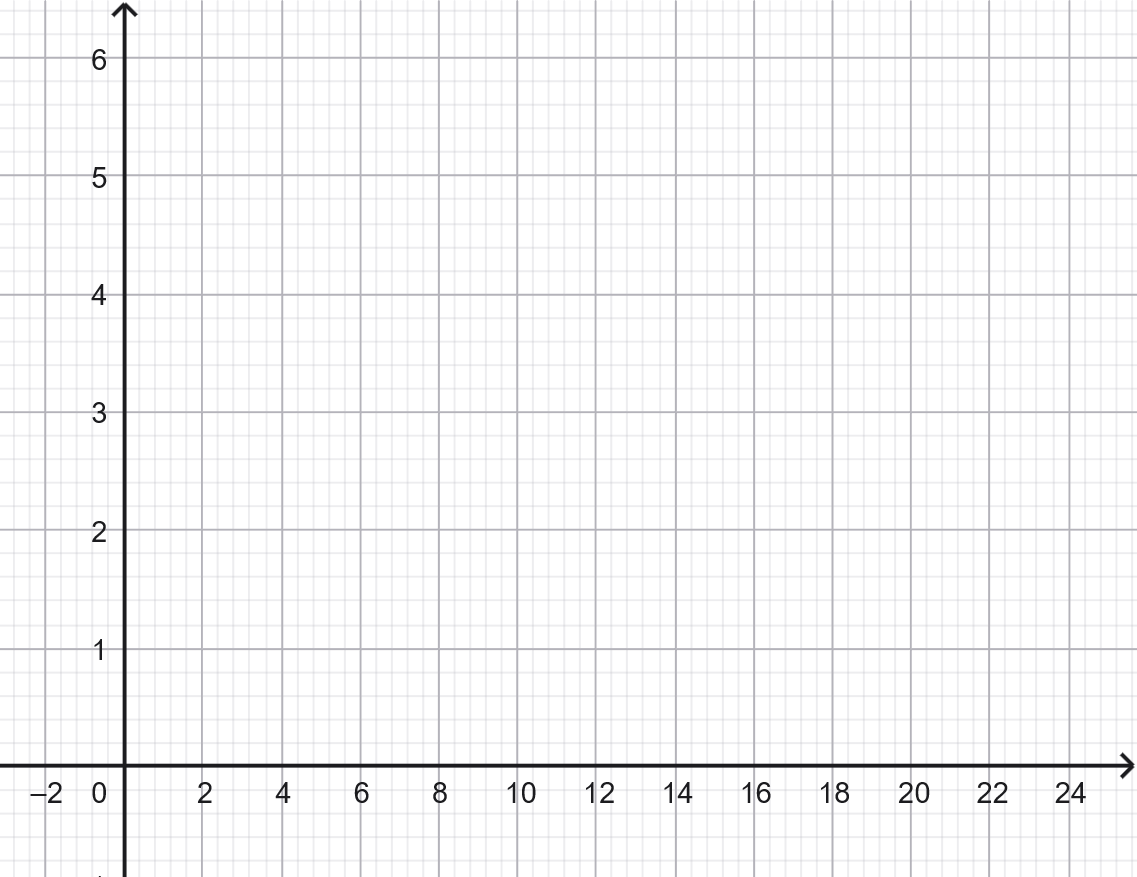
- Lire graphiquement le coût d'un trajet de 15 km.
¶ Exercice 4 – Comparaison de commandes pour le goûter
Une crèche souhaite acheter des compotes et des biscuits pour le goûter.
-
Option A : 0,60 € par compote + 5 € de frais de livraison
-
Option B : 0,50 € par compote + 8 € de frais de livraison
On note :
-
le coût total pour compotes avec l’option A
-
le coût total pour compotes avec l’option B
-
Écrire les expressions de et .
-
Calculer le coût pour 10 compotes et 40 compotes avec chaque option.
-
Tracer les deux fonctions sur Geogebra.
-
Déterminer graphiquement à partir de combien de compotes l’option B devient plus avantageuse que l’option A.
Contenu généré avec l’aide de ChatGPT, révisé et adapté par Thibaut Meunier.
Licence : CC BY-SA 4.0